Model Equivalence using Z3

Most model replacement flows stop after validation accuracy.

If loss and accuracy remain roughly the same, the task is considered done.
But validation only tells us that on the samples we checked the models behave similarly.

It says nothing about the rest of the input space.

Why this matters — two major use cases

There are at least two distinct workflows where this matters:

A) Model pruning / distillation / simplification

We modify a model intentionally:

reduce latency
reduce model size
simplify the architecture (for interpretability or cost)

We want to know if the simplified model really behaves like the original one.

Example: Random Forest → Pruned Random Forest (our example in this post)

B) Model retraining / continuous integration

A model is re-trained with new data, new hyperparams, or a new architecture.

Before replacing the model in production we need to know:

Is the new model equivalent to the legacy one, or where do they differ? How much and where do they differ?

This turns model replacement into a regression test, similar to a CI/CD. This makes model updates less opaque and gives all the scope we need to understand how it generalizes.

Validation tells us similarity on sampled points, on information that we already have.
What we want is equivalence:

For all inputs x in the domain:
    model_A(x) == model_B(x)

If the answer is no, we want to know the exact violating input X.

Z3 for Model Equivalence: Proving ML Models Match (or Finding the exact input where they don’t)

Goal: Instead of measuring similarity between models, prove they’re equivalent, and where they’re not: extract the exact counterexample.

Z3 is a constraint solver from Microsoft Research.
Optimizers try values and adjust based on results.
Z3 doesn’t search, it doesn’t brute forces the computation, it reasons about all possible inputs.
We state the rules, and it determines whether any input satisfies them.

For model equivalence, we ask: is there any x where the two models disagree? If yes, Z3 returns that x; if not, it proves none exists.

The classic use case (or at least how I first heard of z3): Sudoku solver.

Every rule is encoded as a constraint: numbers 1–9, unique rows, unique cols, etc.
Z3 doesn’t brute-force — it symbolically prunes entire spaces at once.

We use the same trick here.

Instead of trying inputs until the model fails, we ask Z3:

∃ x   such that   Model_A(x) ≠ Model_B(x)

If yes → Z3 produces that violating x.
If not → Z3 proves no such x exists within the domain.

Encoding a model as logic

Decision trees are perfect for SMT solving because they’re pure conditional logic:

if x[5] <= 0.12:  
   left
else:             
   right
return leaf_label

Z3 can encode every branch of every tree.

Then we assert:

(pred_A(x) != pred_B(x))

and let Z3 do the search.

Code: Locating the exact counterexample

If a single violating input exists, Z3 returns it: guaranteed and verifiable.

from z3 import Real, RealVal, If, And, Or, Sum, Solver, sat

def encode_tree_as_z3(tree, x_vars):
    t = tree.tree_
    L, R = t.children_left, t.children_right
    feat, thr, val = t.feature, t.threshold, t.value

    def go(n):
        if L[n] == R[n]:
            return RealVal(int(val[n][0].argmax()))
        return If(x_vars[feat[n]] <= thr[n],
                  go(L[n]),
                  go(R[n]))
    return go(0)

def encode_forest_avg_vote(rf, x_vars):
    return Sum(*[encode_tree_as_z3(t, x_vars) for t in rf.estimators_]) / len(rf.estimators_)

def z3_label_counterexample(big, pruned, lo, hi):
    d = len(lo)
    x = [Real(f"x{i}") for i in range(d)]
    b = encode_forest_avg_vote(big, x)
    p = encode_forest_avg_vote(pruned, x)

    s = Solver()
    s.add(And(*[(x[i] >= lo[i]) & (x[i] <= hi[i]) for i in range(d)]))
    s.add((b >= 0.5) != (p >= 0.5))

    if s.check() != sat:
        return None
    m = s.model()
    return [float(str(m[xi])) for xi in x]

lo and hi are per-feature min/max bounds Z3 must respect. This prevents it from returning absurd values like x = 10⁹

>>> [-0.965, 0.549, 0.247, 0.589, 0.475, 3.397, ...]

This vector is a real point in feature space that breaks model equivalence.

Minimal explanation trace

We can even trace which removed trees caused the discrepancy:

def trace_disagreement(x_cex, big, pruned, top_k=8):
    xb = x_cex.reshape(1, -1)
    votes = np.array([t.predict(xb)[0] for t in big.estimators_], float)
    removed = [i for i, t in enumerate(big.estimators_) if t not in pruned.estimators_]

    diffs = [(abs(votes.mean() - ((votes.sum() - votes[i])/(len(votes)-1))), i) for i in removed]
    diffs.sort(reverse=True)
    print(diffs[:top_k])

This produces a ranked list of the trees that mattered with respect to the divergence of the two models.

Visualizing the disagreement surface

Interpretation	Image
Where vote probability differs the most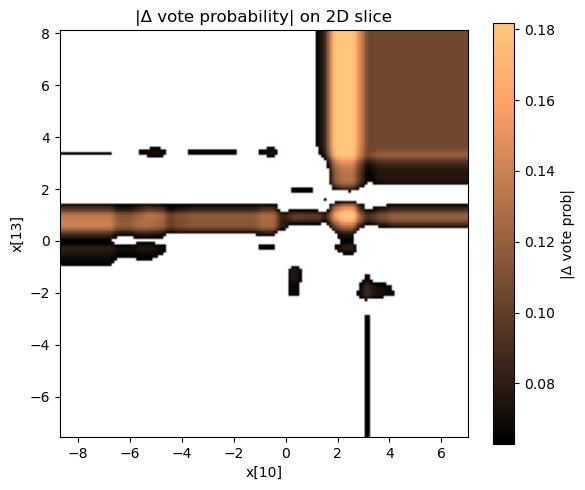
Where the predicted labels actually differ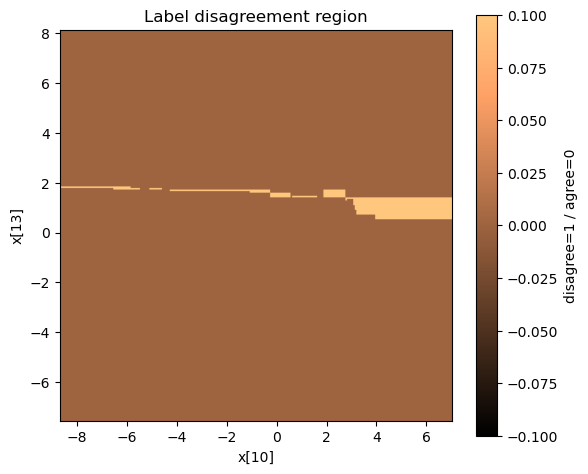
Zoom on violation region with arbitrary difference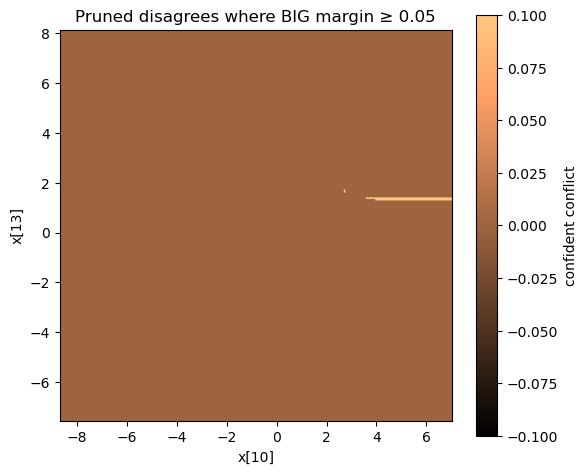

These visuals are easy to track, and with some work, creating something for the most problematic combinations of features, would be very revealing for the pruning process.

Most of the input space is essentially the same, but we see precise “fault lines” where pruning changes the target predictions.

Why this matters

Approach	Guarantees?	Finds exact failure case?
Validation set	No	No
Z3	Yes	Always if exists

Validation gives confidence, Z3 gives certainty.

Closing Remarks

We can formally prove two models behave identically.
Use it to validate pruning / distillation work.
Use it to guard model retraining in CI/CD.
If models diverge, Z3 gives the input that caused the divergence.

No brute force,no test dataset guesses.

Just mathematically guaranteed model equivalence (or a counterexample).