—Detecting Overconfidence with Z3 title: “Detecting Overconfidence with Z3” excerpt: “2025-11-12 — Formally proving overconfidence in ML models using Z3, calibration, and CEGIS-generated counterexamples.” header: overlay_image: /assets/images/z3_overconfidence/header.png tags:
- z3
- machine-learning
- calibration share: true subscribe: true comments: false —
Detecting Overconfidence with Z3
Formal guarantees for calibration — and counterexamples.
Machine-learning models lie.
Not deliberately, but probabilistic outputs often look more certain than reality. Softmax confidence and accuracy are not the same thing, yet we treat confidence as if it were calibrated likelihood.
This post shows a formal method to detect overconfidence using:
Calibration (empirical Lower Confidence Bounds)
Z3 SMT solver (“does any bin violate calibration?”)
CEGIS (CounterExample Guided Inductive Synthesis) to generate a real input that triggers the violation
We don’t just detect miscalibration.
We prove that the model can enter a region where it claims higher confidence than the empirical accuracy supports — and construct an actual input that forces it.
1) Calibration as a contract
From validation data, we derive a simple rule:
“When the model looks like this, its true accuracy is at least X%.”
We group predictions into bins using features like predicted confidence, logit margin, entropy, etc.
For each bin we compute:
- mean confidence
- observed accuracy
- Lower Confidence Bound (Wilson interval) — a conservative estimate
Example (digits model):
bin | conf | LCB | support
----+------+-----+---------
3 | 0.76 | 0.79 | 173
Meaning:
“If the model outputs ~0.76 confidence, accuracy is ≥0.79 with 95% confidence.”
That is a contract.
Calibration visualization
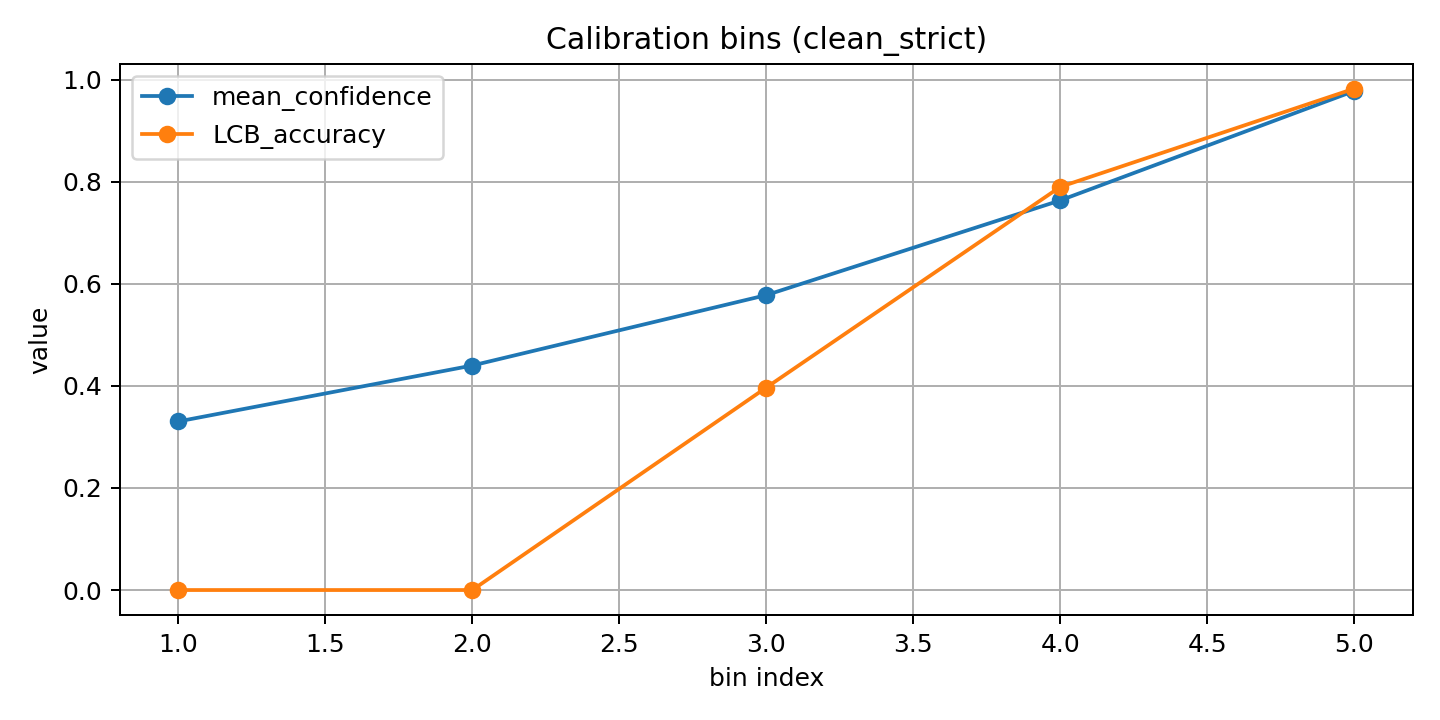
Here confidence (blue) roughly tracks empirical accuracy (orange).
Looks calibrated.
But… visual inspection is not a proof.
2) Z3: “does any bin violate the contract?”
We express the calibration rule as SMT constraints:
# exists bin b where model_confidence > LCB(b) + epsilon
Bin = BoolVector("Bin", num_bins)
s = Solver()
for b in range(num_bins):
s.add(Implies(Bin[b], conf[b] > LCB[b] + epsilon))
s.add(Implies(Bin[b], support[b] >= min_support))
s.add(Or(Bin))
If Z3 returns sat, a violating bin exists.
We now know: there is a region of model behavior where confidence > accuracy
But that’s still abstract — “behavior space”, not input space.
3) Z3 + CEGIS: Generate the input that triggers overconfidence
CEGIS loop:
- Z3 finds a target probability vector
p*inside a violating bin. - We optimize over input space (using gradients) to make the model output
softmax(x) ≈ p*. - If we reach the bin → counterexample found.
Example outputs (real, from this exercise):
Out-of-distribution shift

Model claims 0.84 confidence for some class,
but the calibration LCB for that region is ~0.05.
Confidence inflation (temperature hacking)

Model outputs high confidence by construction —
accuracy does not follow.
Even in the “clean” case

Even a calibrated model can be forced to enter a violating region.
Calibration from validation data ≠ calibration across input space.
Takeaways
Calibration by itself is not a guarantee. With Z3, we turn calibration into a contract, and then break it formally.
| Step | What happens |
|---|---|
| Calibration | “In this confidence region, accuracy ≥ X%” |
| Z3 | “Is there a bin where confidence > X%?” |
| CEGIS | “Here is the input that makes it happen.” |
Calibration literature only measures miscalibration.
Adversarial literature finds perturbations.
Here we prove existence and construct it.
If your model expresses confidence, be suspicious.