Code: github.com/mpcsb/tb-embedding-quality
Why this matters
We tend to treat cosine distance as if it were a true metric.
Cosine does not satisfy triangle inequality: explicitly proven here.
Metric indexes do rely on triangle inequality to prune search space, shown in
Efficient Metric Indexing for Similarity Search.
Metric indexing relies on triangle inequality for pruning.
HNSW / FAISS don’t require strict metric axioms, but they assume neighborhood consistency: if a point is “closer,” greedy search expects it to lead to even closer points.
That assumption only holds when the embedding space has stable geometry (i.e. distances behave consistently like in a true metric).
What causes the embedding geometry to break down
Two independent things:
-
Bad corpus / domain mismatch
If the embedding model wasn’t trained on similar text, semantics get scattered. -
Compression (PCA + quantization)
Removes structure. Local neighborhoods collapse. This is particularly bad because compression solves a lot of operational problems.
Both lead to the same consequences:
- nearest neighbors stop being nearest
- triangle inequality fails locally, and fails harder as distances increase.
- retrieval (the R in RAG) becomes unstable
This post measures that directly.
Setup
We embed two different datasets:
| Corpus | What it contains | Notes |
|---|---|---|
| food | short ingredient / composition snippets | noisy, repetitive text |
| medical | clinical trial abstracts | dense, clean text |
Three embedding variants:
| Name | Model | Dim | Notes |
|---|---|---|---|
A_raw |
DistilBERT STS-B | 768 | strong baseline, ‘high’ dimension |
B_raw |
MiniLM-L6-v2 | 384 | common model in local/demo RAG systems |
B_pca64q4 |
MiniLM → PCA 64 → 4-bit | 64 | aggressive compression |
Each corpus was chunked into 1000 samples.
What we measure
For each point i:
- find its top-k nearest neighbors (
j) - check if any neighbor of a neighbor (
k) breaks triangle inequality:
d(i, k) > d(i, j) + d(j, k) + τ
If no violation exists, the point is clean.
The metric:
clean_frac = fraction of points with consistent neighborhoods
τ = tolerance.
Higher clean_frac: stable space.
Lower clean_frac: distances are not reliable.
I use Z3 only to answer a yes/no question:
“Does any violating (j, k) exist for this anchor?”
Brute-forcing all (i, j, k) triples did not work well when I tackled this in the past.
Z3 doesn’t brute force. It treats distances as constraints and either:
- finds a violating triplet, or
- proves that none exists for that anchor.
Results
Three parts:
1) UMAP: do embeddings even cluster coherently?
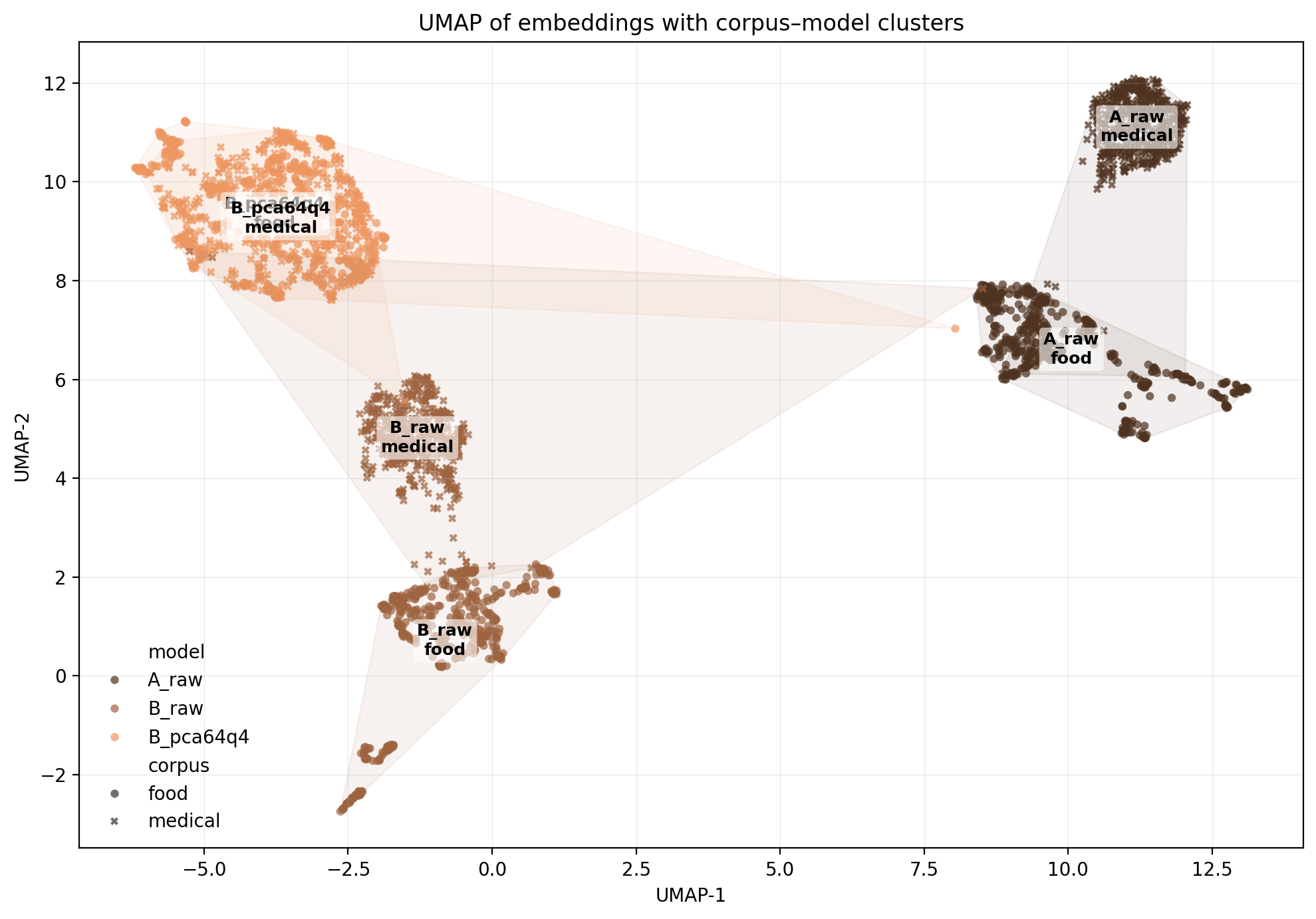
Raw embedding models produce tight clusters separated by corpus, whereas PCA+quantization blurs everything together causing the food and medical corpora to overlap with no separation!
Already looks like geometry degradation.
2) Heatmap: metric stability across k neighbors and τ tolerance
(In the heatmap, the horizontal axis is the neighbor count k and the vertical axis is the tolerance τ. Color indicates the fraction of points that remain clean)
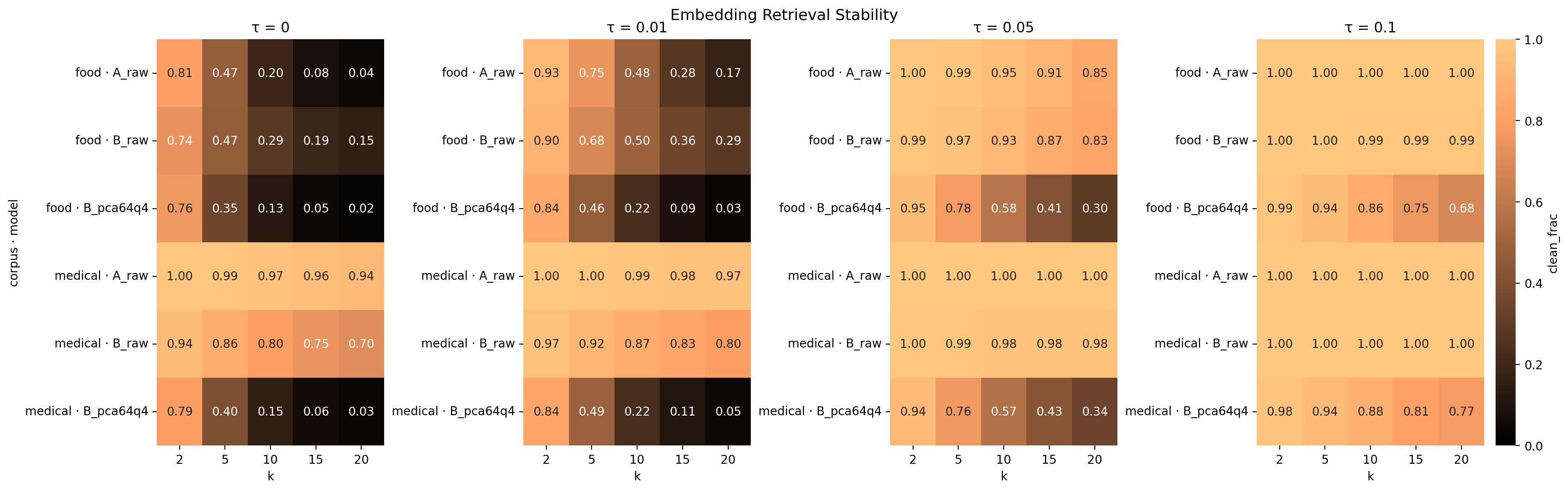
Observations:
- medical corpus: solid geometry (clean_frac ≈ 1.0)
- food corpus: noisy semantics, which leads to poor geometry
- PCA+quantized: catastrophic collapse
Even at τ = 0.1 (a huge forgiveness margin), PCA+quantized still breaks.
3) Stability vs k: how fast the neighborhood falls apart
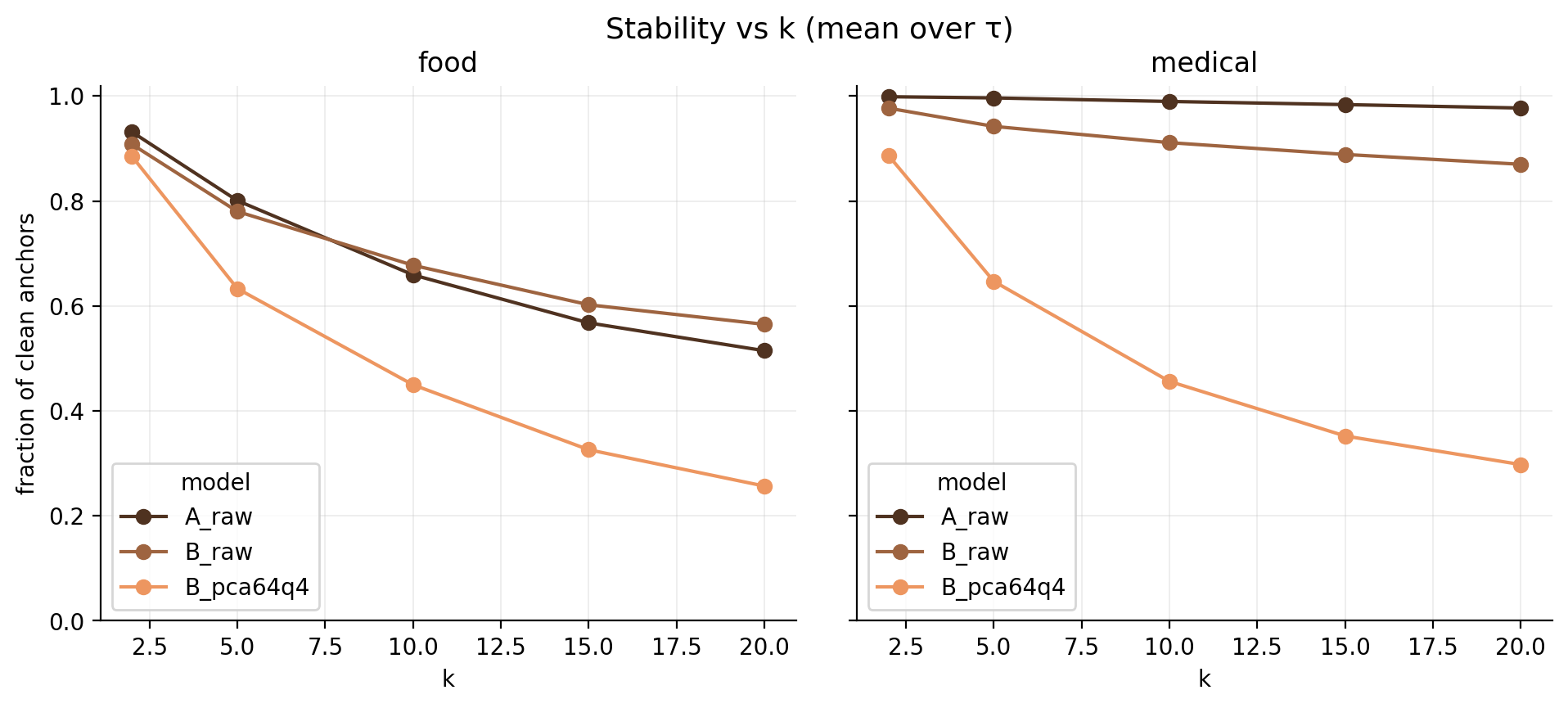
- raw embeddings degrade slowly as k expands
- compressed embedding collapses by k=10
If retrieval expands k during rerank / recall-then-rerank — expect garbage neighbors.
Key takeaways
-
Embeddings are not guaranteed to form a metric space.
If triangle inequality fails, nearest neighbors may not be the nearest.
Retrieval results may not be ideal. -
Compression destroys neighborhood structure.
PCA+quantization doesn’t ‘reduce redundancy’. This step needs extra monitoring, as results can degrade fast. -
Weaker/less structured corpus result garbage geometry.
Not surprising.
Choose embeddings based on how well they preserve geometry.
Vector DBs assume a metric space.
Most embedding models don’t always return one.
If the embedding space breaks (wrong model, wrong corpus, or compression) nearest neighbors aren’t nearest and the R in RAG stands for roulette…