(This post comes from a series of old notebook ideas I’m revisiting — notes written years ago, now turned into posts.)
Why measure information loss when adding noise?
A post on Cook’s blog showed how rounding numeric values can act as a simple form of privacy.
That idea caught my attention: rounding is just a deterministic way of adding noise.
So how much information do we actually lose when we do this?
This note looks answers that question.
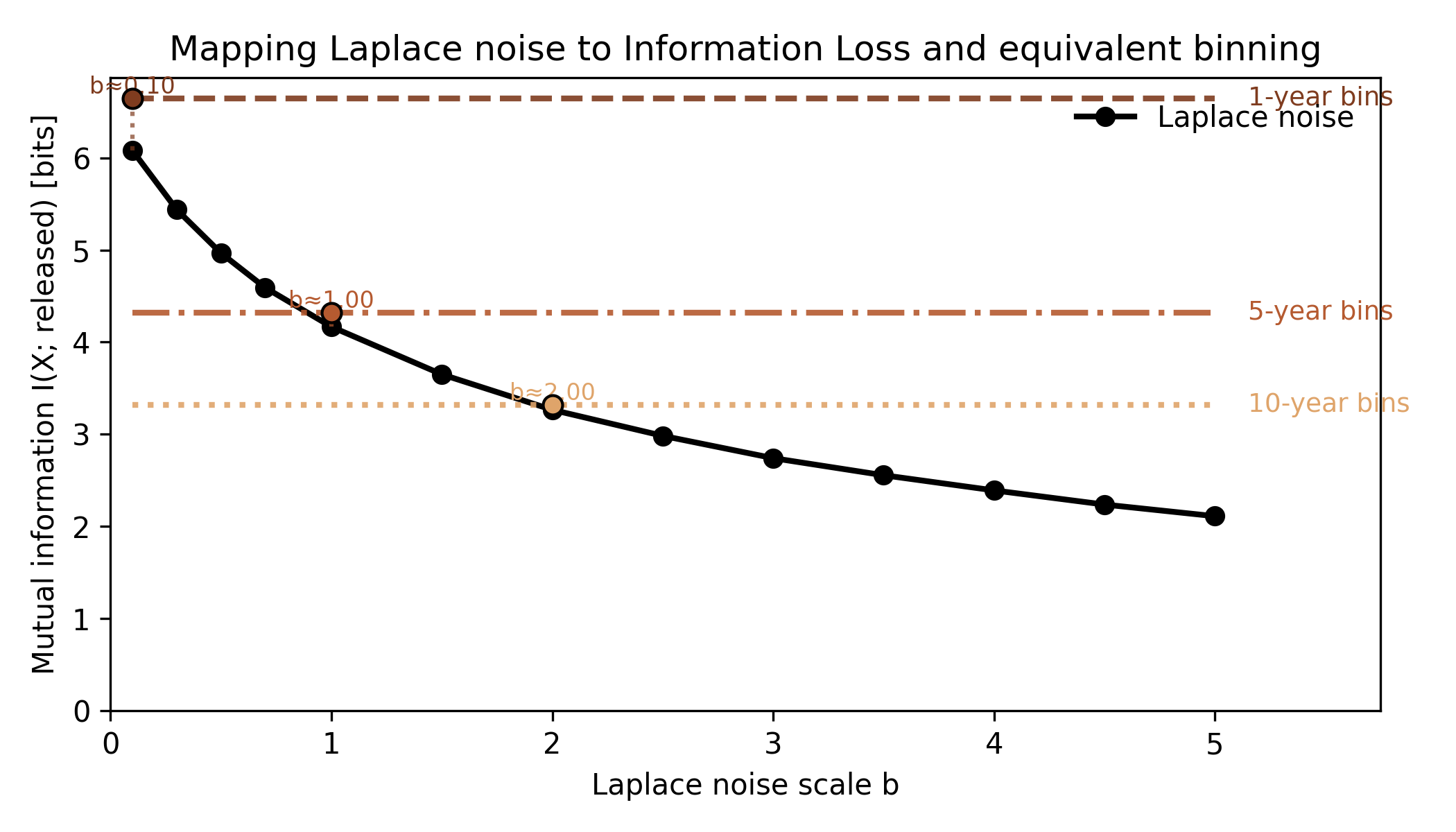
By adding Laplace noise (a common way to blur numeric data: small shifts most of the time, big ones only occasionally) of different magnitudes to a set of “ages” and measuring the mutual information with the original data, we can see how information degrades as noise grows and how that compares to ordinary binning.
Each noise scale b has an equivalent bin width: the point where both destroy the same amount of information.
Setup
We’ll start with a simple “age” variable drawn from a synthetic distribution, from 0-100. More realistic distributions seemed to reach roughly the same conclusions.
To each value, we add Laplace noise with different scales b, and measure how much mutual information remains between the noisy and original data.
For comparison, we also apply deterministic binning: rounding ages into 1-, 5-, and 10-year intervals.
This acts as an upper bound on what the same magnitude of noise would erase.
The figure below maps the two: every noise scale b has an equivalent bin width where the information loss matches.
Results
Information drops smoothly as the noise scale increases.
Small b values barely affect it, but once the noise exceeds a few years, most detail is gone.
The horizontal lines show fixed widths for comparison.
Each crosses the Laplace curve at the point where both destroy the same amount of information which is a practical way to read noise as “effective resolution”.
Noise defines an implicit resolution, which is how precisely a value can still be inferred, and binning defines it explicitly.
Both erase the same amount of information, but they’re effectively not the same operation.
When you bin, you restrict knowledge to a clear interval: “this person is between 25 and 30”. When you add noise, you blur every point independently — sometimes within that window, sometimes beyond it.
Both limit what can be learned, but only noise introduces uncertainty.
Binning is limited by the units we already use: we can round ages to years or to 5-year groups, but can not be smaller than the base unit.
Noise isn’t bound by that because it can be arbitrarily small or large, adjusting precision continuously rather than in discrete steps.
Final remarks
-
Noise and binning set resolution differently.
One continuous, one discrete — both shape how much detail survives. -
Noise is tunable.
Its scale b acts as a continuous knob on effective precision, unlike fixed bins. -
Information loss is measurable.
Mutual information quantifies how much structure the data retain after perturbation. -
At large noise scales, precision saturates.
Beyond the data’s natural granularity, extra noise only adds randomness.