Why study model calibration under noisy data?
A few years ago, Claudia Perlich wrote on Quora that “linear models are surprisingly resilient to noisy data.”
That line stuck with me because it contradicts the common instinct to reach for deeper or more powerful models when the data gets messy.
I wanted to revisit that claim, reproduce it in a small controlled setup, and then extend it a bit:
What happens when we add feature noise instead of switching labels?
And how does calibration (how well predicted probabilities align with reality) break down under both types of noise?
TL;DR
- Linear models degrade gracefully when noise increases; their bias acts as regularization.
- Tree ensembles hold AUC longer under moderate feature noise, but their calibration collapses faster.
- Once labels are corrupted, no model survives: information is lost, not just hidden.
- Calibration helps, but only while the underlying signal still exists.
Approach
The idea was to simulate a clean, linearly separable world and then contaminate it in a controlled way.
- Data: 10 features, 5 informative, synthetic binary target generated with the
make_classificationmethod from sklean. - Noise:
- Label noise: randomly flipping 0↔1 with probability p.
- Feature noise: adding Gaussian or Laplace perturbations, scaled to each feature’s standard deviation.
- Models:
Logistic regression, Random Forest, and XGBoost, with and without isotonic calibration. - Metrics:
AUC for discrimination; Expected Calibration Error (ECE) for reliability.
Each configuration was run over multiple seeds and averaged, using up to 3 000 samples per run.
Results
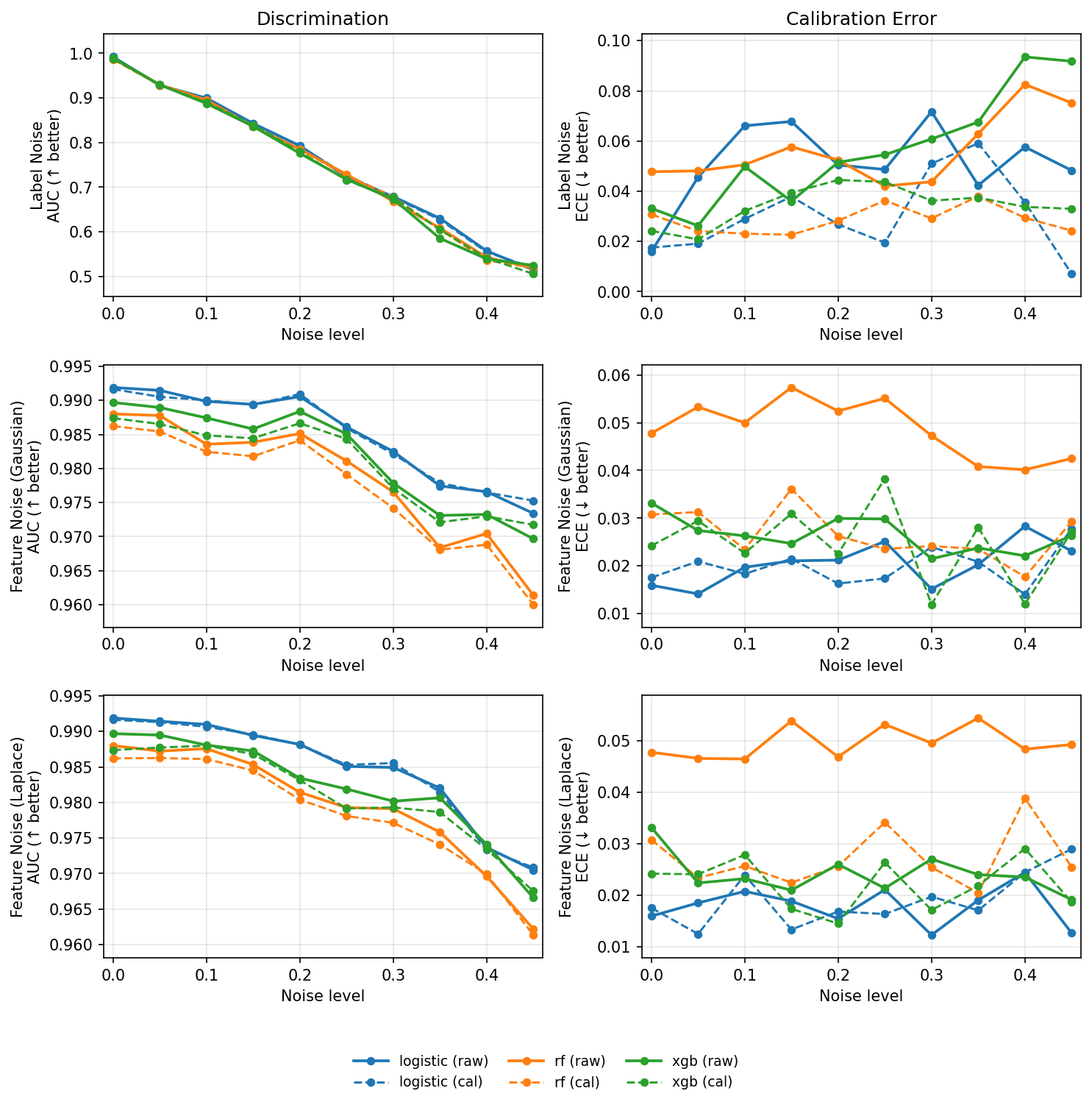
At first glance, intuition is confirmed:
- Under label noise, all models decay in lock-step. Logistic doesn’t collapse faster than the trees; they all converge toward randomness once the labels stop meaning anything.
- Under feature noise, the picture splits:
- Logistic remains smooth and predictable. Its linear boundary blurs but doesn’t overreact (much).
- RF and XGB start to memorize noise, retaining slightly higher AUC for a while but paying for it in calibration error.
- Calibration (the dashed lines) restores some sanity, but only when the signal is still recoverable.
The curves are remarkably smooth, with no weird bumps, no instability.
Simple models with strong inductive bias prefer signal over noise.
Why is the linear model so stable here?
Because the underlying data was generated by a linear process. The logistic model has the right inductive bias — it assumes the true decision boundary is linear; so even as we inject random perturbations, it degrades gracefully.
Tree-based models, are flexible enough to “explain” small fluctuations as structure. That flexibility becomes a liability under noise: they overfit spurious splits, yielding high confidence on wrong examples, which shows up as poor calibration.
In the real world, this pattern often repeats: if your features already capture the main signal, linear baselines are hard to beat on stability. Complexity rarely saves you from bad data.
Conclusion
This small experiment validates Perlich’s observation and extends it slightly:
noise doesn’t just make you wrong, it makes you confident in the wrong things.
Linear models trade expressive power for robustness.
Tree ensembles fight noise longer, but they start lying about their certainty.
Check the code and adjust noise distributions, switch datasets, try out different models. Have fun!